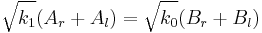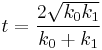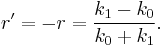Solution of Schrödinger equation for a step potential
The Schrödinger equation for a one dimensional step potential is a model system in quantum mechanics and scattering theory. The problem consists of solving the time-independent Schrödinger equation for a particle with a step-like potential in one dimension. Typically, the potential is modeled as a Heaviside step function.
Contents |
Calculation
The time-independent Schrödinger equation for the wave function 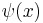 is
is
where  is the Hamiltonian,
is the Hamiltonian, 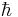 is the (reduced) Planck constant,
is the (reduced) Planck constant,  is the mass,
is the mass,  the energy of the particle and
the energy of the particle and
is the potential step with height 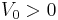 .
. 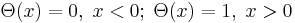 is the Heaviside step-function. The barrier is positioned at
is the Heaviside step-function. The barrier is positioned at 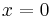 . Without changing the results, any other shifted position was possible. The first term in the Hamiltonian,
. Without changing the results, any other shifted position was possible. The first term in the Hamiltonian, 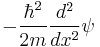 is the kinetic energy.
is the kinetic energy.
The step divides the space in two parts (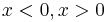 ). In any of these parts the potential is constant meaning the particle is quasi-free, and the solution of the Schrödinger equation can be written as a superposition of left and right moving waves (see free particle)
). In any of these parts the potential is constant meaning the particle is quasi-free, and the solution of the Schrödinger equation can be written as a superposition of left and right moving waves (see free particle)
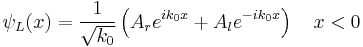 ,
,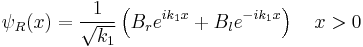
where the wave vectors are related to the energy via
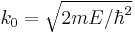 , and
, and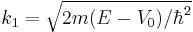 .
.
The index r/l on the coefficients A and B denotes the direction of the velocity vector. Note that for energies 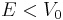 , the wave function to the right of the step is exponentially decaying over a distance
, the wave function to the right of the step is exponentially decaying over a distance  . Nevertheless we keep the notation r/l even though the waves are not propagating anymore in this case. The prefactor
. Nevertheless we keep the notation r/l even though the waves are not propagating anymore in this case. The prefactor 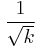 ensures correct normalization.
ensures correct normalization.
The coefficients 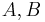 have to be found from the boundary conditions of the wave function at
have to be found from the boundary conditions of the wave function at 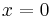 . The wave function and its derivative have to be continuous everywhere, so:
. The wave function and its derivative have to be continuous everywhere, so:
 ,
, .
.
Inserting the wave functions, the boundary conditions give the following restrictions on the coefficients
Transmission and reflection
At this point, it is instructive to compare the situation to the classical case. In both cases, the particle behaves as a free particle outside of the barrier region. A classical particle with energy  larger than the barrier height
larger than the barrier height 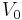 will be slowed down but never reflected by the barrier, while a classical particle with
will be slowed down but never reflected by the barrier, while a classical particle with 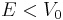 incident on the barrier from the left would always get reflected.
incident on the barrier from the left would always get reflected.
To study the quantum case, let us consider the following situation: a particle incident on the barrier from the left side (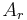 ). It may be reflected (
). It may be reflected (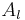 ) or transmitted (
) or transmitted ( ). Here and in the following assume
). Here and in the following assume 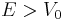
To find the amplitudes for reflection and transmission for incidence from the left, we put in the above equations 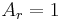 (incoming particle),
(incoming particle), 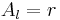 (reflection),
(reflection),  =0 (no incoming particle from the right) and
=0 (no incoming particle from the right) and  (transmission). We then solve the set of two linear equations for
(transmission). We then solve the set of two linear equations for  .
.
The result is:
The model is symmetric with respect to a mirror transformation and at the same time exchange  . For incidence from the right we have therefore the amplitudes for transmission and reflection
. For incidence from the right we have therefore the amplitudes for transmission and reflection
Analysis of the expressions
In this energy range the transmission and reflection coefficient differ from the classical case. They are the same for incidence from the left and right and read, respectively, as
In the limit of large energies  , we have
, we have  and the classical result (T=1, R=0) is recovered. Thus there is a finite probability for a particle with an energy larger than the step height to be reflected.
and the classical result (T=1, R=0) is recovered. Thus there is a finite probability for a particle with an energy larger than the step height to be reflected.
Applications
The Heaviside step potential mainly serves as an exercise in quantum mechanics classes as the solution requires the understanding of a variety of concepts of quantum physics like normalization, matching of wave functions, reflection/transmission amplitudes, and probabilities.
A similar problem to the one considered appears in the physics of normal-metal superconductor interfaces. Quasiparticles are scattered at the pair potential which in the simplest model may be assumed to have a step-like shape. The solution of the Bogoliubov-de Gennes equation resembles that of the discussed Heaviside-step potential. In the superconductor normal-metal case this gives rise to Andreev reflection.
![H\psi(x)=\left[-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}%2BV(x)\right]\psi(x)=E\psi(x),](/2012-wikipedia_en_all_nopic_01_2012/I/bd8542a4b9ae43b36ffe93890fa428a2.png)